Validation of the Koopman's Theorem in DFT by Means of the Calculation of the Conceptual DFT Descriptors of Three Fluorescent DNA Staining Dyes
Juan Frau, Francisco Muñoz and Daniel Glossman- Mitnik
DOI10.21767/2470-6973.100021
Juan Frau1, Francisco Munoz1 and Daniel Glossman- Mitnik1,2*
1Departament de Quimica, Universitat de les Illes Balears, 07122 Palma de Mallorca, Spain
2Laboratorio Virtual NANOCOSMOS, Centro de Investigacion en Materiales Avanzados, Chihuahua, Chih 31136, Mexico
- Corresponding Author:
- Daniel Glossman-Mitnik
Departament de Quimica, Universitat de les Illes
Balears, 07122 Palma de Mallorca, Spain.
Tel: 526144391151
E-mail: daniel.glossman@cimav.edu.mx
Received date: October 10, 2016; Accepted date: October 26, 2016; Published date: November 15, 2016
Citation: Frau J, Munoz F, Mitnik DG. Validation of the Koopmans Theorem in DFT by Means of the Calculation of the Conceptual DFT Descriptors of Three Fluorescent DNA Staining Dyes. Chem Inform. 2016, 2:2. doi:10.21767/2470-6937.100021
Abstract
The fulfillment of the "Koopmans' theorem in DFT" is verified by means of the calculation of several global descriptors arising from Conceptual DFT. They have been calculated through a ΔSCF procedure, and by means of the HOMO and LUMO frontier orbitals. The latest Minnesota family of density functionals has been considered and three fluorescent DNA staining dyes have been studied: Hoechst 33258, Hoechst 33342 and Hoechst 34580. On the basis of the obtained Conceptual DFT indices, a series of descriptors have been devised in order to determine the accuracy of each model chemistry considered here in the verification of the mentioned theorem. It is shown that the only density functionals that fulfill this task are those denoted as range-separated hybrids (RSH), while the local density functionals are not useful at all.
Keywords
Computational chemistry; Molecular modeling; DNA staining dyes; Conceptual DFT; Chemical reactivity theory
Introduction
Conceptual Density Functional Theory (DFT) or Chemical Reactivity Theory (as it is also known) is a powerful tool for the prediction, analysis and interpretation of the outcome of chemical reactions [1-4].
Following the pioneering work of Parr and others [1], a useful number of concepts have been derived from the analysis of the density of any molecular system through DFT. These concepts that allow a researcher to make qualitative predictions about the chemical reactivity of a given system can also be quantified and are collectively known as Conceptual DFT Descriptors.
In order to obtain quantitative values of the Conceptual DFT Descriptors, it is necessary to resort to the Kohn-Sham theory trough calculations of the molecular density, the energy of the system, and the orbital energies in particular, those related to the frontier orbitals, that is, HOMO and LUMO [5-10].
The usual way to proceed implies as a first step the choice of model chemistry for the study of the molecular system or chemical reaction of interest. Model chemistry is a combination of a density functional, a basis set, and an implicit solvent model that one consider that can be adequate for the problem under study. There is a plethora of information in the literature about how to choose this model chemistry and one generally follows the experience of previous researchers and his/her own work.
Although the foundations of DFT have established that a universal density functional must exist, and that all of the properties of the system can be obtained through calculations with this functional, in practice one needs to resort to some of the approximate density functional that have been developed during the last thirty years. Due to the fact that these are approximate functional (that is, not a universal functionals), many of them are good for predicting some properties and others are good for another properties. Sometimes, you can find density functionals that are excellent for describing the properties of a given molecular system with a particular functional group, but it is necessary to resort to other density functionals for a different functional group that you want to include in the molecular system under study.
When one is dealing with the study of the chemical reactivity, that is, a process that involve the transference of electrons, it is usual to perform calculations not only of the ground state, but also for open systems like the radical cation and radical anion. These systems are often difficult to converge giving trustworthy results, specially if diffuse functions must be included in the basis set [5-10]. For this reason, it is convenient to have a method that can give all information that one needs directly from the results of the calculation of the ground state of the molecular system under study. In particular, one may want to obtain the ionization potential (I) and electron affinity (A) of the system avoiding the calculation of the radical’s anion and cation. Indeed, the link for this s given by the so-called Koopmans' theorem [7-10], that states that within Hartree-Fock (HF) theory, the I can be approximated by minus the energy of the HOMO, that is, I=-εH. By extension, it is considered that the A can be approximated by minus the energy of the LUMO, that is, A=-εL.
However, the validity of the Koopmans' theorem in DFT is controversial and the problem has been identified with the difference between the fundamental band gap and the HOMO-LUMO gap that is called the derivative discontinuity. Notwithstanding, it has been mentioned recently [11] that an exact physical meaning can be assigned to the Kohn-Sham (KS) HOMO using "the KS analog of Koopmans' theorem in Hartree- Fock theory", which states that for the exact theory, the KS HOMO is equal to and opposite of the ionization potential, εH=-I [12-15]. Due to the mentioned problem of the discontinuity, a similar Koopmans' theorem that relates the LUMO energy to the electron affinity does not exist. Thus, it has been proposed to circumvent the problem, to consider that the I of the N+1 electron system (the anion) is the same that the A of N electron system [11]. By considering range-separated hybrids (RSH) functional [16-18], where the repulsive Coulomb potential is split into a long-range (LR) and short-range (SR) term, e.g., via r-1=r-1erf(ϒr)+r-1 erfc(ϒr), with ϒ the range-separation parameter, Kronik et al. [11] showed that with a judicious choice of this last parameter, the validity of the Koopmans' theorem could be enforced.
This ϒ tuning technique can be used for the improvement of the description of the properties predicted by these density functionals. This is a consequence of the better fulfillment of the Koopmans' theorem that leads to better agreement of the orbital energies with the I and A. For example, Lima et al. [19] have recently presented an improved description of the optical properties of carotenoids by tuning some long-range corrected functionals.
This means that the goodness of a given density functional can be estimated can be estimated by checking how well it follows the "Koopmans' theorem in DFT" that makes it behave closer to the exact density functional, and this will be crucial for a good calculation of the Conceptual DFT descriptors that predict and explain the chemical reactivity of molecular systems. However, the ϒ tuning procedure for the RSH density functionals is system dependent and that implies that different density functionals are going to be used for the calculation of the descriptors for the different molecular systems. Thus, it will be interesting to study other RSH density functional where the parameter is fixed by constructions, although other parameters have been fitted to reproduce some molecular properties. In particular, we are going to consider several density functionals that have shown great accuracy across a broad spectrum of databases in chemistry and physics [20].
The aim of this work is to conduct a comparative study of the performance of the latest Minnesota family of density functionals for the calculation of the Conceptual DFT descriptors of three fluorescent DNA staining dyes: Hoechst 33258 (HD33258) [21], Hoechst 33342 (HD33342) [21] and Hoechst 34580 (HD34580) [21] whose molecular structures are shown in Figures 1-3. These dyes have important applications in detecting nucleic acids, cancer cells, human papilloma virus (HPV), nucleic acid quantification, detecting abnormal gametes, apoptosis, polynucleotides, proteins and peptides, Alzheimer's disease, treating of cancer and detecting malaria infected red blood cells [21].
Theoretical Background
Within the conceptual framework of DFT [2,22], the chemical potential μ, which measures the escaping tendency of electron from equilibrium, is defined as:
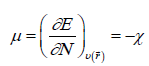 (1)
(1)
Where χ is the electronegativity.
The global η hardness can be seen as the resistance to charge transfer:
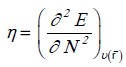 (2)
(2)
Using a finite difference approximation and Koopmans' theorem [7-10], the above expressions can be written as:
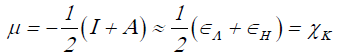 (3)
(3)
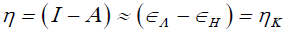 (4)
(4)
Where εH and εL are the energies of the highest occupied and the lowest unoccupied molecular orbitals, HOMO and LUMO, respectively.
The electrophilicity index ω has been defined as:
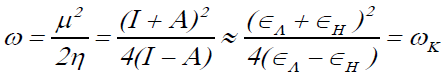 (5)
(5)
The electrodonating (ω-) and electroaccepting (ω+) powers have been definedp as [23]:
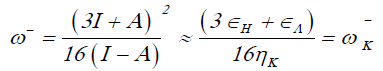 (6)
(6)
And
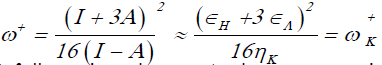 (7)
(7)
It follows that a larger ω+ value corresponds to a better capability of accepting charge, whereas a smaller value of ω- value of a system makes it a better electron donor. In order to compare ω+ with ω-, the following definition of net electrophilicity has been proposed [24]:
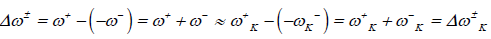 (8)
(8)
That is, the electroaccepting power relative to the electrodonating power.
Settings and Computational Methods
All computational studies were performed with the Gaussian 09 [25] series of programs with density functional methods as implemented in the computational package. The equilibrium geometries of the molecules were determined by means of the gradient technique. The force constants and vibrational frequencies were determined by computing analytical frequencies on the stationary points obtained after the optimization to check if there were true minima. The basis set used in this work was Def2SVP for geometry optimization and frequencies while Def2TZVP was considered for the calculation of the electronic properties [26,27].
For the calculation of the molecular structure and properties of the studied systems, we have chosen several density functionals from the Minnesota density functionals family, which consistently provide satisfactory results for several structural and thermodynamic properties [20]: M11, which is a is a rangeseparated hybrid meta- GGA [28], M11L, which is a dual-range local meta-GGA [29], MN12L, which is a nonseparable local meta-NGA [30], MN12SX, which is a range-separated hybrid nonseparable meta-NGA [31], N12, which is a nonseparable gradient approximation [32], N12SX, which is a range-separated hybrid nonseparable gradient approximation [31], SOGGA11, which is a GGA density functional [33] and SOGGA11X, which is a hybrid GGA density functional [34]. In these functionals, GGA stands for generalized gradient approximation (in which the density functional depends on the up and down spin densities and their reduced gradient) and NGA stands for nonseparable gradient approximation (in which the density functional depends on the up/down spin densities and their reduced gradient, and also adopts a nonseparable form). All the calculations were performed in the presence of water as a solvent, by doing IEFPCM computations according to the SMD solvation model [35].
Results and Discussion
The molecular structures of HD33258, HD33342 and HD34580 were pre-optimized by starting with the readily available MOL structures, and finding the most stable conformers by means of the Avogadro 1.2.0 program [36,37] through a random sampling with molecular mechanics techniques and a consideration of all the torsional angles. The structures of the resulting conformers were then reoptimized with the M11, M11L, MN12L, MN2SX, N12, N12SX, SOGGA11 and SOGGA11X density functionals in conjunction with the Def2SVP basis set and the SMD solvation model, using water as a solvent.
The HOMO and LUMO orbital energies (in eV), ionization potentials I and electron a nities A (in eV), and global electronegativity χ, total hardness η, global electrophilicity ω, electrodonating power, (ω-), electroaccepting power (ω+), and net electrophilicity Δω± of the HD33258, HD33342 and HD34580 molecules calculated with the M11, M11L, MN12L, MN12SX, N12, N12SX, SOGGA11, and SOGGA11X density functionals and the Def2TZVP basis set using water as solvent simulated with the SMD parameterization of the IEF-PCM model are presented in Tables 1-3, respectively. The upper part of the tables shows the results derived assuming the validity of Koopmans' theorem in DFT (hence the subscript K) and the lower part shows the results derived from the calculated vertical I and A.
| Property | M11 | M11L | MN12L | MN12SX | N12 | N12SX | SOGGA11 | SOGGA11X |
|---|---|---|---|---|---|---|---|---|
| HOMO | -4.519 | -2.491 | -2.170 | -2.496 | -2.113 | -2.410 | -2.453 | -3.096 |
| LUMO | 0.377 | -1.831 | -1.446 | -1.515 | -1.540 | -1.469 | -1.881 | -0.834 |
| χK | 2.071 | 2.161 | 1.808 | 2.006 | 1.826 | 1.940 | 2.167 | 1.965 |
| ωK | 4.896 | 0.661 | 0.724 | 0.981 | 0.573 | 0.940 | 0.573 | 2.262 |
| ωK | 0.438 | 3.535 | 2.259 | 2.050 | 2.911 | 2.001 | 4.100 | 0.854 |
| ωK- | 2.218 | 8.191 | 5.466 | 5.164 | 6.770 | 5.030 | 9.320 | 2.831 |
| ωK+ | 0.147 | 6.030 | 3.658 | 3.158 | 4.944 | 3.090 | 7.153 | 0.866 |
| ωK± | 2.365 | 14.221 | 9.125 | 8.323 | 11.714 | 8.120 | 16.473 | 3.697 |
| I | 2.439 | 2.621 | 2.272 | 2.453 | 2.278 | 2.350 | 2.624 | 2.336 |
| A | 1.718 | 1.670 | 1.311 | 1.566 | 1.326 | 1.536 | 1.670 | 1.616 |
| χ | 2.079 | 2.146 | 1.792 | 2.010 | 1.802 | 1.943 | 2.147 | 1.976 |
| η | 0.720 | 0.951 | 0.961 | 0.887 | 0.951 | 0.814 | 0.954 | 0.720 |
| ω | 2.999 | 2.419 | 1.699 | 2.277 | 1.707 | 2.319 | 2.415 | 2.712 |
| ω- | 7.083 | 5.971 | 4.295 | 5.614 | 4.374 | 5.661 | 5.963 | 6.457 |
| ω+ | 5.004 | 3.825 | 2.503 | 3.605 | 2.572 | 3.718 | 3.816 | 4.481 |
| Δω± | 12.088 | 9.796 | 6.798 | 9.219 | 6.946 | 9.379 | 9.379 | 10.937 |
Table 1. HOMO and LUMO orbital energies (in eV), ionization potentials I and electron affinities A (in eV), and global electronegativity χ , total hardness η global elec-trophilicity ω, electroaccepting power (ω+), and net electrophilicity Δ ω± of HD33258 calculated with the M11, M11L, MN12L, MN12SX, N12, N12SX, SOGGA11 and SOGGA11X density functionals and the Def2TZVP basis set using water as as solvent simulated with the SMD parametrization of the IEF-PCM model. The upper part of the table shows the results derived assuming the validity of Koopmans' theorem and the lower part shows the results derived from the calculated vertical I and A.
| Property | M11 | M11L | MN12L | MN12SX | N12 | N12SX | SOGGA11 | SOGGA11X |
|---|---|---|---|---|---|---|---|---|
| HOMO | -7.529 | -4.859 | -4.611 | -5.124 | -4.204 | -4.847 | -4.490 | -5.914 |
| LUMO | 0.156 | -2.282 | -1.874 | -1.844 | -2.026 | -1.795 | -2.342 | -1.047 |
| χK | 3.687 | 3.571 | 3.242 | 3.484 | 3.115 | 3.321 | 3.416 | 3.481 |
| ωK | 7.686 | 2.577 | 2.737 | 3.281 | 2.178 | 3.053 | 2.148 | 4.867 |
| ωK | 0.884 | 2.474 | 1.92 | 1.850 | 2.228 | 1.806 | 2.715 | 1.245 |
| ωK- | 4.092 | 6.894 | 5.632 | 5.647 | 6.149 | 5.464 | 7.273 | 4.534 |
| ωK+ | 0.405 | 3.324 | 2.390 | 2.163 | 3.034 | 2.143 | 3.857 | 1.053 |
| ωK± | 4.497 | 10.218 | 8.022 | 7.811 | 9.183 | 7.607 | 11.130 | 5.587 |
| I | 5.451 | 5.033 | 4.768 | 5.101 | 4.442 | 4.815 | 4.754 | 5.161 |
| A | 1.731 | 2.116 | 1.727 | 1.878 | 1.802 | 1.842 | 2.122 | 1.760 |
| χ | 3.591 | 3.575 | 3.248 | 3.489 | 3.122 | 3.328 | 3.438 | 3.460 |
| η | 3.721 | 2.918 | 3.041 | 3.223 | 2.640 | 2.973 | 2.632 | 3.401 |
| ω | 1.733 | 2.190 | 1.734 | 1.889 | 1.846 | 1.863 | 2.246 | 1.760 |
| ω- | 5.494 | 6.349 | 5.283 | 5.724 | 5.417 | 5.576 | 6.374 | 5.463 |
| ω+ | 1.903 | 2.774 | 2.035 | 2.235 | 2.295 | 2.248 | 2.937 | 2.003 |
| Δω± | 7.396 | 9.123 | 7.317 | 7.959 | 7.713 | 7.824 | 9.311 | 7.466 |
Table 2. HOMO and LUMO orbital energies (in eV), ionization potentials I and electron affinities A (in eV), and global electronegativity χ, total hardness η global elec-trophilicity ω, electroaccepting power (ω+), and net electrophilicity Δ ω± of HD33258 calculated with the M11, M11L, MN12L, MN12SX, N12, N12SX, SOGGA11 and SOGGA11X density functionals and the Def2TZVP basis set using water as as solvent simulated with the SMD parametrization of the IEF-PCM model. The upper part of the table shows the results derived assuming the validity of Koopmans' theorem and the lower part shows the results derived from the calculated vertical I and A.
| Property | M11 | M11L | MN12L | MN12SX | N12 | N12SX | SOGGA11 | SOGGA11X |
|---|---|---|---|---|---|---|---|---|
| HOMO | -7.317 | -4.749 | -4.496 | -5.010 | --4.141 | -4.758 | -4.417 | -5.740 |
| LUMO | 0.255 | -2.185 | -1.781 | -1.750 | -1.919 | -1.697 | -2.236 | -0.950 |
| χK | 3.531 | 3.467 | 3.138 | 3.380 | 3.030 | 3.227 | 3.326 | 3.345 |
| ωK | 7.572 | 2.564 | 2.715 | 3.259 | 2.222 | 3.061 | 2.181 | 4.791 |
| ωK | 0.823 | 2.344 | 1.814 | 1.752 | 2.066 | 1.701 | 2.536 | 1.168 |
| ωK- | 3.885 | 6.581 | 5.367 | 5.399 | 5.787 | 5.208 | 6.872 | 4.308 |
| ωK+ | 0.354 | 3.114 | 2.229 | 2.019 | 2.757 | 1.980 | 3.546 | 0.963 |
| ωK± | 4.239 | 9.696 | 7.596 | 7.417 | 8.543 | 7.188 | 10.418 | 5.270 |
| I | 5.248 | 4.868 | 4.600 | 4.997 | 4.297 | 4.743 | 4.585 | 5.167 |
| A | 1.636 | 2.023 | 1.639 | 1.785 | 1.701 | 1.745 | 2.024 | 1.659 |
| χ | 3.442 | 3.445 | 3.119 | 3.391 | 2.999 | 3.244 | 3.304 | 3.413 |
| η | 3.612 | 2.846 | 2.961 | 3.212 | 2.596 | 2.998 | 2.560 | 3.508 |
| ω | 1.640 | 2.086 | 1.643 | 1.791 | 1.732 | 1.755 | 2.133 | 1.661 |
| ω- | 5.227 | 6.072 | 5.031 | 5.477 | 5.126 | 5.320 | 6.077 | 5.247 |
| ω+ | 1.785 | 2.627 | 1.912 | 2.086 | 2.127 | 2.076 | 2.773 | 1.834 |
| Δω± | 7.013 | 8.699 | 6.943 | 7.564 | 7.254 | 7.395 | 8.850 | 7.081 |
Table 3. HOMO and LUMO orbital energies (in eV), ionization potentials I and electron affinities A (in eV), and global electronegativity χ, total hardness η global elec-trophilicity ω, electroaccepting power (ω+), and net electrophilicity Δ ω± of HD33258 calculated with the M11, M11L, MN12L, MN12SX, N12, N12SX, SOGGA11 and SOGGA11X density functionals and the Def2TZVP basis set using water as as solvent simulated with the SMD parametrization of the IEF-PCM model. The upper part of the table shows the results derived assuming the validity of Koopmans' theorem and the lower part shows the results derived from the calculated vertical I and A.
Inspired from previous works on this subject [11,19], and with the object of analyzing our results in order to verify the fulfillment of the "Koopmans' theorem in DFT", we have designed several descriptors that relate the results obtained through the HOMO and LUMO calculations with those obtained by means of the vertical I and A with a ΔSCF procedure. However, it must be stressed that it is not our intention to perform a gap-fitting by minimizing a descriptor by choosing optimal range-separation parameter γ, but to check if the density functionals considered in this study, in which, some of the contain a fixed range-separation parameter γ, obbey the "Koopmans' theorem in DFT". As a matter fact, there is no range-separation parameter γ in our designed descriptors. Moreover, we have considered A as minus the energy of the LUMO of the neutral system instead of considering A as minus the energy of the HOMO of the N+1 electron system, as it was in the mentioned works [11,19].
The first three descriptors are related to the simplest fulfillment of the Koop-mans' theorem by relating εH with -I, εL with -A, and the behavior of them in the description of the band gap:
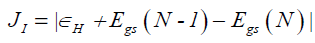 (9)
(9)
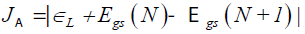 (10)
(10)
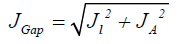 (11)
(11)
Next, we consider four other descriptors that analyze how well the studied density functionals are useful for the prediction of the electronegativity χ, the global hardness η and the global electrophilicity ω, and for a combination of these Conceptual DFT descriptors, just considering the energies of the HOMO and LUMO or the vertical I and A:
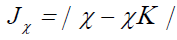 (12)
(12)
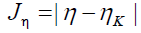 (13)
(13)
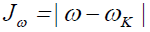 (14)
(14)
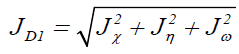 (15)
(15)
Where D1 stands for the first group of Conceptual DFT descriptors. Finally, we designed other four descriptors to verify the goodness of the studied density functionals for the prediction of the electroaccepting power ω+, the electrodonating power ω-, the net electrophilicity Δω±, and for a combination of these Conceptual DFT descriptors, just considering the energies of the HOMO and LUMO or the vertical I and A:
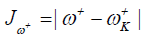 (16)
(16)
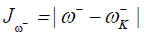 (17)
(17)
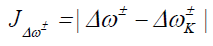 (18)
(18)
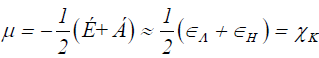 (19)
(19)
Where D2 stands for the first group of Conceptual DFT descriptors. The results of the calculations of JI, JA, JGap, Jχ, Jη, Jω, JD1, Jω+,Jω-, JΔω± and JD2 for the HD33258, HD33342 and HD34580 molecules are displayed in Tables 4-6, respectively.
| Atom | M11 | M11L | MN12L | MN12SX | N12 | N12SX | SOGGA11 | SOGGA11X |
|---|---|---|---|---|---|---|---|---|
| JI | 2.081 | 0.130 | 0.102 | 0.043 | 0.165 | 0.060 | 0.171 | 0.760 |
| JA | 2.095 | 0.161 | 0.135 | 0.051 | 0.214 | 0.067 | 0.211 | 0.782 |
| JGap | 2.953 | 0.207 | 0.170 | 0.067 | 0.270 | 0.089 | 0.272 | 1.091 |
| Jχ | 0.007 | 0.016 | 0.017 | 0.004 | 0.024 | 0.004 | 0.020 | 0.011 |
| Jη | 4.176 | 0.291 | 0.237 | 0.094 | 0.378 | 0.126 | 0.382 | 1.542 |
| Jω | 2.561 | 1.115 | 0.589 | 0.227 | 1.204 | 0.319 | 1.686 | 1.858 |
| JD1 | 4.899 | 1.153 | 0.635 | 0.246 | 1.262 | 0.343 | 1.728 | 2.415 |
| Jω+ | 4.865 | 2.220 | 1.172 | 0.450 | 2.396 | 0.632 | 3.357 | 3.625 |
| Jω- | 4.858 | 2.204 | 1.155 | 0.446 | 2.372 | 0.628 | 3.337 | 3.615 |
| JΔω± | 9.723 | 4.425 | 2.327 | 0.896 | 4.768 | 1.260 | 6.695 | 7.240 |
| JD2 | 11.908 | 5.419 | 2.850 | 1.097 | 5.839 | 1.543 | 8.199 | 8.867 |
Table 4. Descriptors JI, JA, JGap, Jχ, Jη, Jω, JD1, Jω+,Jω-, JΔω± and JD2 for the HD33258 molecule calculated from the results of Table 1.
As can be seen from Tables 1-3, and the results presented in Tables 4-6, the "Koopman's theorem in DFT" holds with great accuracy for the MN12SX and N12SX density functionals, which are a range-separated hybrid meta-NGA and a range-separated hybrid NGA density functionals, respectively. Indeed, the values of JI, JA and JGap are not exactly zero. However, their values can be favorably compared with the results presented for these quantities in the work of Lima et al. [19], where the minima has been obtained by choosing a parameter that enforces that behavior.
| Atom | M11 | M11L | MN12L | MN12SX | N12 | N12SX | SOGGA11 | SOGGA11X |
|---|---|---|---|---|---|---|---|---|
| JI | 2.078 | 0.174 | 0.157 | 0.024 | 0.238 | 0.033 | 0.264 | 0.753 |
| JA | 1.887 | 0.167 | 0.146 | 0.034 | 0.224 | 0.047 | 0.220 | 0.713 |
| JGap | 2.807 | 0.241 | 0.215 | 0.042 | 0.327 | 0.058 | 0.343 | 1.037 |
| Jχ | 0.096 | 0.004 | 0.006 | 0.005 | 0.007 | 0.007 | 0.022 | 0.020 |
| Jη | 3.965 | 0.341 | 0.304 | 0.058 | 0.462 | 0.080 | 0.483 | 1.466 |
| Jω | 0.849 | 0.284 | 0.186 | 0.039 | 0.382 | 0.057 | 0.470 | 0.516 |
| JD1 | 4.056 | 0.444 | 0.356 | 0.070 | 0.600 | 0.099 | 0.674 | 1.554 |
| Jω+ | 1.401 | 0.545 | 0.350 | 0.077 | 0.732 | 0.112 | 0.899 | 0.929 |
| Jω- | 1.497 | 0.549 | 0.355 | 0.072 | 0.739 | 0.105 | 0.921 | 0.950 |
| JΔω± | 2.899 | 1.095 | 0.705 | 0.148 | 1.471 | 0.217 | 1.819 | 1.879 |
| JD2 | 3.551 | 1.341 | 0.863 | 0.182 | 1.801 | 0.266 | 2.228 | 2.301 |
Table 5. Descriptors JI, JA, JGap, Jχ, Jη, Jω, JD1, Jω+,Jω-, JΔω± and JD2 for the HD33342 molecule calculated from the results of Table 2.
| Atom | M11 | M11L | MN12L | MN12SX | N12 | N12SX | SOGGA11 | SOGGA11X |
|---|---|---|---|---|---|---|---|---|
| JI | 2.068 | 0.120 | 0.104 | 0.013 | 0.156 | 0.015 | 0.168 | 0.573 |
| JA | 1.891 | 0.162 | 0.142 | 0.035 | 0.218 | 0.048 | 0.211 | 0.710 |
| JGap | 2.803 | 0.202 | 0.176 | 0.037 | 0.268 | 0.050 | 0.270 | 0.912 |
| Jχ | 0.089 | 0.021 | 0.019 | 0.011 | 0.031 | 0.016 | 0.022 | 0.068 |
| Jη | 3.960 | 0.282 | 0.246 | 0.048 | 0.374 | 0.063 | 0.379 | 1.283 |
| Jω | 0.817 | 0.258 | 0.171 | 0.038 | 0.334 | 0.054 | 0.404 | 0.493 |
| JD1 | 4.044 | 0.383 | 0.300 | 0.062 | 0.503 | 0.085 | 0.554 | 1.376 |
| Jω+ | 1.342 | 0.509 | 0.336 | 0.079 | 0.660 | 0.112 | 0.795 | 0.871 |
| Jω- | 1.431 | 0.488 | 0.317 | 0.067 | 0.629 | 0.095 | 0.773 | 0.871 |
| JΔω± | 2.773 | 0.997 | 0.653 | 0.146 | 1.289 | 0.207 | 1.568 | 1.811 |
| JD2 | 3.397 | 1.221 | 0.799 | 0.179 | 1.579 | 0.254 | 1.920 | 2.218 |
Table 6. Descriptors JI, JA, JGap, Jχ, Jη, Jω, JD1, Jω+,Jω-, JΔω± and JD2 for the HD34580 molecule calculated from the results of Table 3.
It is interesting to see that the same density functionals also fulfill the "Koop-mans' theorem in DFT" for the other descriptors, namely Jχ, Jη, Jω and JD1 as well as for Jω-,Jω+, JΔω±, and JD2. These results are very important, because they show that it is not enough to rely only in JI, JA and JGap. For example, if we consider only Jχ, for all of the density functionals considered, the values are very close to zero. As for the other descriptors, only the MN12SX and N12SX density functionals show this behavior. That means that the results for Jχ are due to a fortituous cancellation of errors.
The usual GGA (SOGGA11) and hybrid-GGA (SOGGA11X) are not good for the fulfillment of the "Koopmans' theorem in DFT", and the same conclusion is valid for the local functionals M11L, MN12L and N12.
An important fact is that although the range-separated hybrid NGA and range-separated hybrid meta-NGA density functionals can be useful for the calculation of the Conceptual DFT descriptors, it is not the same for the range-separated hybrid GGA (M11) density functional. An inspection of Tables 1-3 shows that this is due to the fact that this functional describes inadequately the energy of the LUMO, leading to negative values of A, which are in contradiction with the ΔSCF results.
Conclusion
From the whole of the results presented in this contribution it has been clearly demonstrated that the chemical reactivity of the HD33258, HD33342 and HD34580 molecules can be predicted by using DFT-based reactivity descriptors such as the electronegativity, global hardness, global electrophilicity, electrodonating and electroaccepting powers, and net electrophilicity.
The Minnesota family of density functionals (M11, M11L, MN12L, MN12SX, N12, N12SX, SOGGA11 and SOGGA11X) have been tested for the fulfillment of the "Koopmans' theorem in DFT" by comparison of the HOMO- and LUMO-derived values with those obtained through a ΔSCF procedure. It has been shown that the range-separated hybrid meta-NGA density functional (MN12SX) and the range-separated hybrid NGA density functional (N12SX) are the best for the accomplishment of this objective. As such, they are a good alternative to those density functionals whose behavior have been tuned through a gap-fitting procedure and a good prospect for their usefulness in the description of the chemical reactivity of molecular systems of larger size.
Acknowledgements
This work has been partially supported by CIMAV, SC and Consejo Nacional de Ciencia y Tecnolog a (CONACYT, Mexico) through Grant 219566/2014 for Basic Science Research and Grant 265217/2016 for a Foreign Sabbatical Leave. Daniel Glossman- Mitnik conducted this work while a Sabbatical Fellow at the University of the Balearic Islands from which support is gratefully acknowl-edged. This work was cofunded by the Ministerio de Economia y Competitividad (MINECO) and the European Fund for Regional Development (FEDER) (CTQ2014-55835-R).
References
- Parr R, Yang W (1989) Density-Functional Theory of Atoms and Molecules. Oxford University Press, New York, USA.
- Geerlings P, Proft DF, Langenaeker W (2003) Conceptual Density Functional Theory. Chemical Reviews 103: 1793-1873.
- Toro LA (2007) Theoretical Aspects of Chemical Reactivity. Vol. 19, Elsevier Science, Amsterdam.
- Chattaraj P (2009) Chemical Reactivity Theory - A Density Functional View. CRC Press. Taylor & Francis Group, Boca Raton.
- Huzinaga S, Andzelm J, Klobukowski M, Radzio-Audzelm E, Sakai Y (1984) Gaussian Basis Sets for Molecular Calculations. Elsevier.
- Easton R, Giesen D, Welch A, Cramer C, Truhlar D (1996) The MIDI! Basis Set for Quantum Mechanical Calculations of Molecular Geometries and Partial Charges. Theoretical Chemistry Accounts 93: 281-301.
- Lewars E (2003) Computational Chemistry - Introduction to the Theory and Applications of Molecular and Quantum Mechanics. Kluwer Academic Publishers, Dordrecht.
- Young D (2001) Computational Chemistry - A Practical Guide for Applying Techniques to Real-World Problems. John Wiley & Sons.
- Jensen F (2007) Introduction to Computational Chemistry. 2nd edn. John Wiley & Sons, Chichester, England.
- Cramer C (2004) Essentials of Computational Chemistry - Theories and Models. 2nd edn. John Wiley & Sons, Chichester, England.
- Kronik L, Stein T, Refaely AS, Baer R (2012) Excitation Gaps of Finite-Sized Systems from Optimally Tuned Range-Separated Hybrid Functionals. Journal of Chemical Theory and Computation 8: 1515-1531.
- Perdew J, Parr R, Levy M B (1982) Density-Functional Theory for Fractional Particle Number: Derivative Discontinuities of the Energy. Physical Review Letters 49: 1691-1694.
- Almbladh CO, Barth UV (1985) Exact Results for the Charge and Spin Densities, Exchange-Correlation Potentials, and Density-Functional Eigen-values. Physical Review B 31: 3231-3244.
- Perdew J, Burke K, Ersernh M (1997) Erratum: Generalized Gradient Approximation Made Simple. Physical Review Letters 78: 1396.
- Levy M, Perdew JP, Sahni V (1984) Exact Differential Equation for the Density and Ionization Energy of a Many Particle System. Physical Review 30: 2745-2748.
- Savin A (2011) Beyond the Kohn - Sham Determinant. In: Recent Advances in Density Functional Methods. World Scienti 4: 129-153.
- Leininger T, Stoll H, Werner HJ, Savin A (1997) Combining Long-Range Configuration Interaction with Short-Range Density Functionals. Chemical Physics Letters 275: 151-160.
- Savin A, Flad HJ (1995) Density Functionals for the Yukawa Electron-Electron Interaction. International Journal of Quantum Chemistry 56: 327-332.
- IT Lima, Prado ADS, Martins JBL, Oliveira NPH, Ceschin AM, et al. (2016) Improving the Description of the Optical Properties of Carotenoids by Tuning the Long-Range Corrected Functionals. The Journal of Physical Chemistry A 120: 4944-4950.
- Peverati R, Truhlar DG (2011) Quest for a Universal Density Functional: The Accuracy of Density Functionals across a Broad Spectrum of Databases in Chemistry and Physics. Philosophical Transactions Series A, Mathematical, Physical, and Engineering Sciences, p: 372.
- Sabnis R (2010) Handbook of Biological Dyes and Stains. John Wiley & Sons, Hoboken, New Jersey, USA.
- Parr R, Yang W (1984) Density Functional Approach to the Frontier-Electron Theory of Chemical Reactivity. Journal of the American Chemical Society 10: 4049-4050.
- Gazquez J, Cedillo A, Vela A (2007) Electrodonating and Electroaccepting Powers. Journal of Physical Chemistry 10: 1966-1970.
- Chattaraj P, Chakraborty A, Giri S (2009) Net Electrophilicity. Journal of Physical Chemistry A 37: 10068-10074.
- Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, et al. (2009) Gaussian 09 Revision D 01. Gaussian Inc., Wallingford CT.
- Weigend F, Ahlrichs R (2005) Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy. Physical Chemistry Chemical Physics 7: 3297-3305.
- Weigend F (2006) Accurate Coulomb-fitting Basis Sets for H to R. Physical Chemistry Chemical Physics 8: 1057-1065.
- Peverati R, Truhlar DG (2011) Improving the Accuracy of Hybrid Meta-GGA Density Functionals by Range Separation. The Journal of Physical Chemistry Letters 21: 2810-2817.
- Peverati R, Truhlar DG (2012) M11-L: A Local Density Functional That Provides Improved Accuracy for Electronic Structure Calculations in Chemistry and Physics. The Journal of Physical Chemistry Letters 3: 117-124.
- Peverati R, Truhlar DG (2012) An Improved and Broadly Accurate Local Approximation to the Exchange-Correlation Density Functional: the MN12-L Functional for Electronic Structure Calculations in Chemistry and Physics. Physical Chemistry Chemical Physics 38: 13171-13174.
- Peverati R, Truhlar DG (2012) Screened-Exchange Density Functionals with Broad Accuracy for Chemistry and Solid-State Physics. Physical Chemistry Chemical Physics 47: 16187-16191.
- Peverati R, Truhlar DG (2012) Exchange-Correlation Functional with Good Accuracy for both Structural and Energetic Properties while Depending Only on the Density and Its Gradient. Journal of Chemical Theory and Computation 7: 2310-2319.
- Peverati R, Zhao Y, Truhlar D (2011) Generalized Gradient Approximation That Recovers the Second-Order Density-Gradient Expansion with Optimized Across-the-Board Performance. The Journal of Physical Chemistry Letters 16: 1991-1997.
- Peverati R, Truhlar DG (2011) Communication: A Global Hybrid Generalized Gradient Approximation to the Exchange-Correlation Functional That Satisfies the Second-Order Density-Gradient Constraint and Has Broad Ap-plicability in Chemistry. The Journal of Chemical Physics 135: 191102.
- Marenich A, Cramer C, Truhlar D (2009) Universal Solvation Model Based on Solute Electron Density and a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. Journal of Physical Chemistry 113: 6378-6396.
- Avogadro: An Open - Source Molecular Builder and Visualization Tool - Version 1.2.0 - https://avogadro.openmolecules.net (2016).
- Hanweel M, Lonie D, Vandermeersch T, Zurek E, Hutchison G (2012) Avogadro: An Advanced Semantic Chemical Editor, Visualization and Analysis Platform. Journal of Cheminformatics 4: 17.
Open Access Journals
- Aquaculture & Veterinary Science
- Chemistry & Chemical Sciences
- Clinical Sciences
- Engineering
- General Science
- Genetics & Molecular Biology
- Health Care & Nursing
- Immunology & Microbiology
- Materials Science
- Mathematics & Physics
- Medical Sciences
- Neurology & Psychiatry
- Oncology & Cancer Science
- Pharmaceutical Sciences